This technical note explores the critical role of optical etalons in contemporary laser system technology. They are widely deployed in both industry and research with applications ranging from astronomy, telecommunications, optical fabrication, and spectroscopy.
We provide a comprehensive analysis of their design, operation, and reference applications, ranging from telecommunications to laser precision. It highlights the importance of free spectral range and finesse in etalon performance, along with the meticulous manufacturing required to minimise defects. Gain a deeper understanding of how these precise optical filters are essential in high-precision measurements and advanced scientific research.
Etalons are optical components based on the principle of the Fabry-Perot Interferometer. They are effective narrowband filters, transmitting only light of specific, periodic frequencies with tight bandwidths. They are commonly used in applications such as telecommunications, lasers and spectroscopy.
An Etalon consists of two flat, partially reflecting plates separated by a distance. The gap between them, either in vacuum or filled with air or some solid substrate forms an optical cavity. These two types are known as “Air Spaced” and “Solid” Etalons respectively and possess different advantages and disadvantages.
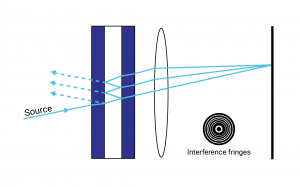
Figure 1: Ray diagram depicting the multiple interference principles of Etalons/Fabry-Perot interferometers
Etalons function as multiple beam interferometers, incident light passes through the first plate and into the cavity at which point it undergoes multiple internal reflections resulting in the transmission of light with many different phases through the whole assembly. Assuming no absorption in the component and equal reflectance off both interfaces in the cavity the resulting transmission is given by the equation:
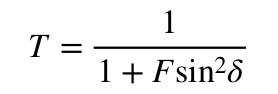
Where
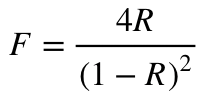
Where R is the reflectance of both surfaces of the cavity and δ is the phase acquired by light passing through the cavity once. F is sometimes known as the “coefficient of finesse”, and is related to an important quantity known as the “Finesse” of an etalon. The transmission curve is given below by figure 2. The multiple beam interference due to reflections within the cavity results in a transmission profile with peaks at δ = mπ where m is an integer. This corresponds to when (at normal incidence) the optical length of the cavity is mλ/2 where λ is the wavelength of the incident light. With increasing F the width of the fringes becomes increasingly narrow.
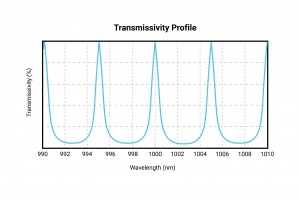
Figure 2: Transmission profile for an ideal Etalon
An important part of the specification of an Etalon is the Free Spectral Range (FSR) which is the separation between the adjacent peaks. FSR for incoming light at normal incidence is given by:
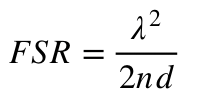
Where n is the refractive index of the cavity and d is the separation of the plates. The ratio of the FSR with the Full Width Half Maximum (an expression for the bandwidth of the transmission peaks, FWHM) is called the “finesse” 
. For sufficiently small δ finesse is given by
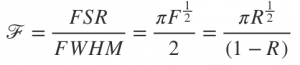
Roughly speaking, the Finesse parametrises the performance of the Etalon as a narrowband filter, with a higher finesse resulting in narrower transmission bands. For high finesse applications dielectric coatings with high reflectance are coated onto the cavity interior to boost reflectance. A high finesse is desirable in spectroscopy and spectrum analysis as the Etalon can possess both a large Free Spectral Range and a small resonator bandwidth allowing for a high spectral resolution. The finesse as a function of plate reflectivity is given by figure 3 below.
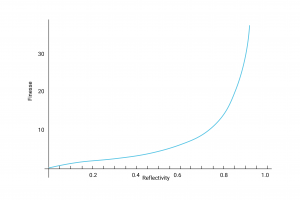Figure 3: Finesse as a function of reflectance
As with all equations in physics, the above all assumes a perfect situation. In reality the actual finesse will be lower than the theoretical reflectivity finesse due to defects and the physical limitations and quality of the assembly components.
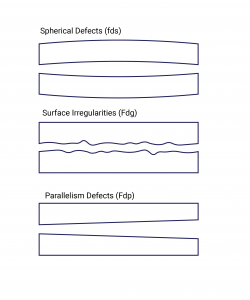
Figure 4: The three principle defects
Figure 4 depicts the three main Etalon defect types. All three defect-types introduce variations in the ideally fixed distance between the Etalon plates, resulting in reduced finesse, peak shifts and lowered resolution. A distinction between the theoretical “reflectivity finesse” and “effective finesse” is then made, the latter quantity representing the finesse of the system taking into account defects. Aside from depending on surface flatness and component tolerances the effective finesse also depends on the clear surface aperture, a smaller aperture leading to a higher finesse.
Another consideration is inhomogeneity in the refractive index of the plates which has a similar effect to flatness limitations and surface irregularity due to deformation in the transmitted wave-front, and the problem worsens the thicker the Etalon plates are. As a result, it is advisable to consider purchasing glass plates with an inhomogeneity grade of 4 or more (as per ISO 10110 Part 4).
If you have any queries about ordering an Etalon then do not hesitate to contact us as at MPO we have an extensive background in the design and manufacturing of Etalons for Solarscopes among other purposes.
References and further reading
Thin Film Optical Filters Third Edition, H. A. Macleod, Institute of Physics publishing, J W Arrowsmith LtD. Bristol, 2001, ISBN 0 7503 06887 2
Handbook of Optical Systems Volume 5, H. Gross (ed.), Wiley-VCH Verlag GmbH & Co KG, 2012, ISBN 978-3-527-40381-3
Optical Interference Coatings, N. Kaiser, H. K. Pulker, Springer-Verlag Berlin Heidelberg 2003, ISBN 3-540-00364-9
Read our insight post recognising the legacy of Charles Fabry and Alfred Perot, on the 125th anniversary of the invention of the optical etalon.