In high-energy laser systems, the precision and efficiency of optical components are paramount. High reflection coatings, interference filters, and bandpass filters play crucial roles in enhancing performance and protecting delicate equipment. These elements ensure that lasers operate at optimal wavelengths and with minimal losses, thereby maximising output and reducing potential damage.
This technical paper delves into the design, application, and benefits of quarter wave stack-based coatings and their used as filters, providing valuable insights for engineers and scientists working with advanced optical systems.
The quarter wave stack is an elegantly simple yet incredibly versatile dielectric multilayer system that forms the basis of optical coatings from high reflection coatings to edge filters and beyond. The quarter wave stack is an optical assembly composed of alternating layers of high and low index dielectric materials with an optical thickness equal to a quarter of a specified design wavelength.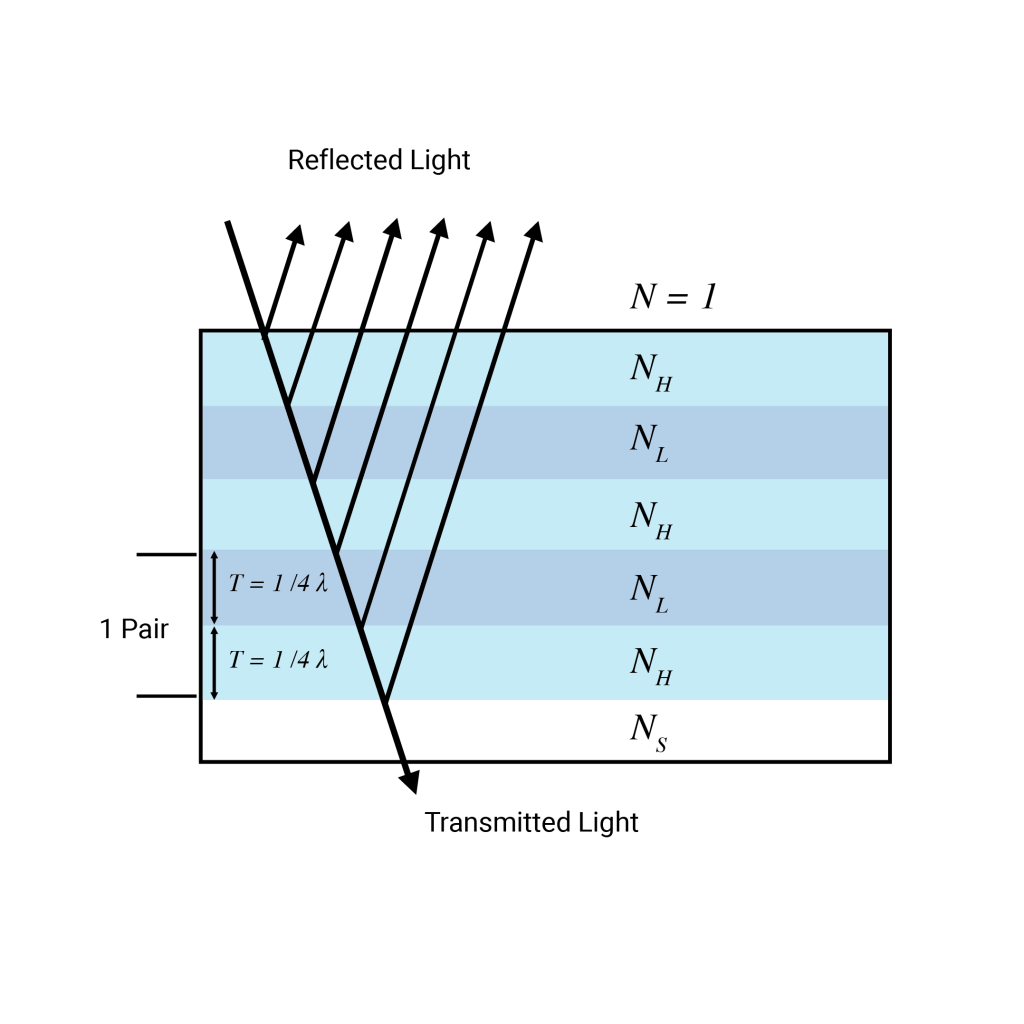
Figure 1: A quarter wave stack consisting of alternating layers of equal thickness and refractive indices NH and NL (where H denotes the “high” index and L denotes the “low” index).
At the design wavelength a quarter wave stack is highly reflecting. The initial reflection of the first layer changes the phase of the first reflected wave by 180° as nAir < nh. The refracted beam reflects off the second layer and does not undergo a phase change as nL < nH but it does travel an extra half wavelength which changes its phase by 180degrees. It therefore constructively interferes with the first reflected wave. At the interface between the second and third layer, the refracted beam travels a full wavelength but undergoes a phase change upon reflection meaning it again constructively interferes. Considering these reflections and refractions iteratively we see that the reflected beams interfere constructively, maximising reflection. The reflectivity of such an arrangement is given by the equation:
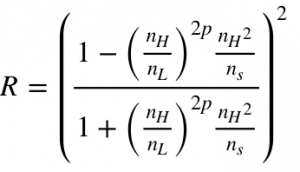
Where ns is the index of refraction of the substrate and 2p+1 is the number of layers. It is easy to see that if the term containing the indices is larger than 1 then increasing the number of pairs of layers increases the reflectivity. Theoretically we could deposit an infinite number of films to achieve absolute reflectance but this would not be feasible in the real world as coating stress, scatter losses etc would outweigh any potential benefit. In reality approximately 30 layers are generally sufficient.
The behaviour of the film over a broadband of wavelengths is given by figure 2:
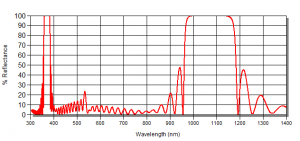
Figure 2: Quarter Wave Stack High Reflector designed for λ = 1064nm. Note the extra peak around λ/3 = 355nm and the shorter peak at λ/2 = 532nm.
Close to the design wavelength the high reflectivity is sustained with the breadth of the reflectivity band dictated by the ratio of the refractive indices of the materials used. The bigger the ratio, the wider the reflectivity band. This rapidly drops off into high transmission oscillations though additional high reflection peaks occur at wavelengths where the layers are an odd number of quarter wavelengths thick. The reflective properties and bandwidth can be further improved if we deviate from the design and modify the thickness’ in accordance with a geometric series.
As indicated, this behaviour makes the quarter wave stack adaptable for use as an edge filter that filters out a section of the electromagnetic spectrum above or below a specified wavelength. These are referred to as long-pass and short-pass filters respectively. The oscillatory behaviour referred to in literature as the “ripple” is however undesirable and the quarter wave stack requires adjustments to reduce it such as the inclusion of matching layers between the multilayer and the substrate/air, or via design optimisation methods. Unwanted reflection bands can also be suppressed to extend high transmission zones.
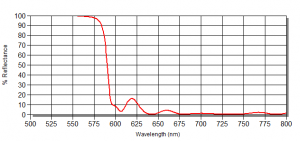
Figure 3: An example of a long-pass edge filter with a boundary between zones at λ = 580nm.
Additionally, a pronounced reflectance peak sometimes referred to as the “2nd harmonic” tends to show up at λ/2 as seen in figure 2. This poses an obvious problem if a quarter wave stack is to be used as a low-pass filter. The peak is sensitive to variations in layer thickness and so can be suppressed by tweaking the design. On the other hand, it can be difficult to remove fully due to very small thickness deviations in the actual coating and in some cases a broadband transmission filter may be specified with an average transmission over the region rather than a lower bound on performance.
Quarter wave stacks or edge filters can additionally be implemented in band-pass filters, which consist of regions of high transmission bounded by regions of rejection. Broad band-pass filters can be achieved via stacking of a long-pass and short-pass filter on the same substrate with spacer layers to suppress interference between the two stacks.
Similar techniques and combinations of stacks can be used in the design of high reflectance dielectric mirrors with multiple design wave-lengths. These kinds of designs are more challenging however due to the number of layers and interference between stacks. Though spacer layers will suppress interference, small errors in layer thickness may reintroduce unwanted transmission or reflection peaks.
At MPO we work with our customers to determine the most suitable optical coatings for their specific applications. With years of experience and an intimate knowledge of thin film coatings design we can produce bespoke, quality coatings according to the specifications you require.
References and further reading
Thin Film Optical Filters Third Edition, H. A. Macleod, Institute of Physics publishing, J W Arrowsmith LtD. Bristol, 2001, ISBN 0 7503 06887 2
A. F. Turner, P. W. Baumeister, Multilayer Mirrors with High Reflectance Over an Extended Spectral Region. Applied Optics, Vol. 5(1), 69-76 (1966)
O. S. Heavens, H. M. Liddell, Staggered Broad-Band Reflecting Multilayers. Applied Optics Vol. 5(3), 373-376 (1966)
H. D. Polster, A Symmetrical All-Dielectric Interference Filter, Rochester, New York, USA. Journal of the Optical Society of America Vol. 42(1), 21-24 (1952)