The index of refraction is a critical factor in laser design and high-energy optics. It controls how light travels through different materials, influencing laser performance, beam quality, and system efficiency. This article delves into the physics of the index of refraction, its dependence on wavelength and material composition, and its impact on optical component design for high-energy laser systems.
The index of refraction or refractive index can be simply defined as the ratio of the speed of light in a vacuum c= 299792458 m/s, generally approximated to 3×10^8m/s, and the speed at which light propagates through the material, i.e. the index of refraction n is given by:
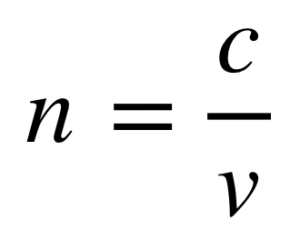
For example, crown glass has an index of refraction n=1.52 meaning that light travels only about 66% of the speed of light in a vacuum whilst travelling through that material. Much of optics comes down to the study of light travelling through media of different refractive indices.
When light is incident upon a dielectric material such as glass, some of the light is reflected at an angle equal to the angle of incidence, and some light is transmitted or “refracted” through at an angle defined by Snell’s law:
n0 sinθr= n1sinθt
Where n0 is the index of refraction of the incident medium, n1 is the index of the refracting medium, θr is the angle of incidence/reflection and θt is the angle at which the light is refracted.
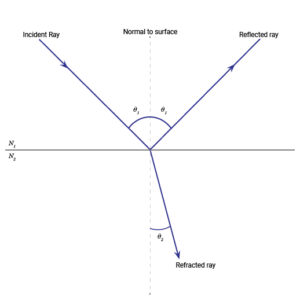
The amount of light that is reflected and transmitted is determined by the so called “Fresnel” equations which will be covered by a future technical note. Additionally, the “phase” of the light is shifted by 180 deg (π/2) when light is reflected of a (dielectric) surface of higher index of refraction, though the refracted light retains the same phase.
Dispersion
The refractive index of a material varies with the wavelength of the light passing through, this is an effect known as dispersion. A well-known, illustrative example of this is white light incident upon a prism. White light is made up of lots of different colours which experience different refractive indices when they enter the prism. Thanks to Snell’s law they will transmit through the prism at different angles and so the white light is split apart.

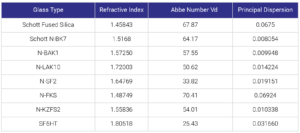
Accounting for dispersion is very important in the design of optical systems, especially those that operate across multiple wavelengths or large bandwidths. In optical coatings the refractive index can also depend on the production process and the exact nature of the coating microstructure. In bulk substrates the dispersion depends on the glass type though it is often low for standard materials like Fused Silica and BK7. In substrate material specifications the dispersion is characterised by a quantity known as the “Abbe number” commonly denoted as Vd. The Abbe number is defined by:
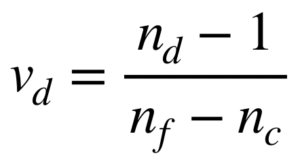
Where nd,f,c is the refractive index value at 587.56nm, 486.13nm and 656.27nm respectively. Glasses characterised by a low index and low dispersion tend to have a high Abbe number, whereas the number is low for high index, high dispersion glasses. The Abbe number along with the principal dispersion nf – nc are of course loose estimates for the characterisation of dispersion. For more details refer to partial dispersions provided by glass manufacturers and the Sellmeier dispersion formula.
Absorption Coefficient
A closely related number to the refractive index is the extinction coefficient commonly denoted by k. The extinction coefficient determines how much the intensity of light is reduced as it penetrates a material, i.e. the absorptance of the material. Together with the index of refraction it constitutes the imaginary part of the “complex refractive index” N=n+ik where i is the imaginary unit. In optics the distinction between dielectrics and metals is that metals have a non-zero extinction coefficient and are hence absorbing whereas dielectrics do not and absorb no light. Like the refractive index, the extinction coefficient can also be dispersive. For example whilst fused silica is an excellent dielectric material across the visible spectrum, it can suddenly become absorbing in the UV.
Realistically many dielectric materials, both substrates and coating materials in fact have small extinction coefficients and so are slightly absorbing. Appropriate choice of material is incredibly important when designing and producing high LIDT parts as even a tiny degree of absorption can have catastrophic results!
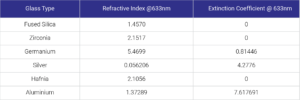
The index of refraction is a cornerstone in the design and optimisation of high-energy laser systems. By carefully considering the refractive properties of materials, engineers and scientists can fine-tune laser systems for maximum efficiency and precision.
References and further reading
Thin Film Optical Filters Third Edition, H. A. Macleod, Institute of Physics publishing, J W Arrowsmith LtD. Bristol (2001), ISBN 0 7503 06887 2
Handbook of Optical Systems Vol. 1, B. Dörband, H. Müller, Wiley-VCH Verlag GmbH & Co. KGaA, Germany, Weinheim (2012) ISBN 978-3-527-40377-6
Handbook of Optical Systems Vol. 5, B. Dörband, H. Müller, Wiley-VCH Verlag GmbH & Co. KGaA, Germany, Weinheim (2012) ISBN 978-3-527-40381-3
M. N. Polyanskiy, “Refractive index database,” https://refractiveindex.info. Accessed on 2020-02-03
TIE-29 Homogeneity of optical glass, Schott AG, Technical Information (2016)
Schott Optical Glass Datasheets, Schott AG (2019)

