Group delay dispersion (GDD) plays a critical role in the performance of ultrafast laser systems, specifically in shaping laser pulses. Understanding how GDD affects pulse duration and waveform is key for optimising laser performance in scientific, medical, and industrial applications. This technical note provides a concise introduction to GDD.
For ultrashort laser pulses, a low group delay dispersion across the operational bandwidth is extremely important as dispersive effects can introduce pulse broadening and other unwanted changes to the beam characteristics. To understand what group delay dispersion is and how it impacts laser performance we must first consider the structure of a laser pulse. A typical model for a laser pulse consists of a plane wave or other oscillating function with a typically Gaussian envelope that localises the pulse in space and time.
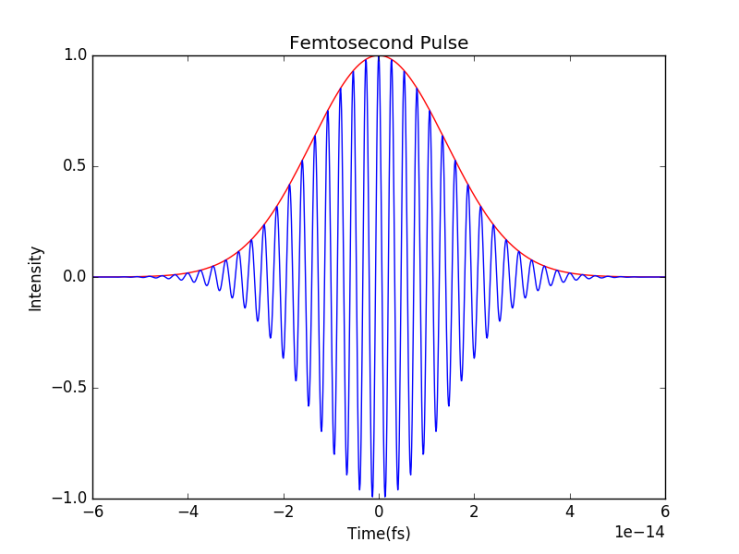
Figure 1: A femtosecond pulse with a gaussian envelope.
A realistic laser pulse will consist of components across a range of frequencies which oscillate and travel independently. To understand the dispersion of these frequencies we expand the phase into a Taylor series φ(ω) of a component about some central frequency ω0:
φ(ω) = φ(ω0) + φ'(ω0)(ω – ω0) + φ”(ω – ω0)2 + . ..
Where ‘ indicates differentiation and . .. indicates higher order terms. The φ'(ω0) is the change in phase with respect to frequency (at centre frequency ω0), known as the group delay, and is generally stated in femtoseconds fs. φ’‘(ω0) is the change in the group delay with respect to frequency (at centre frequency ω0), known as group delay dispersion (abbreviated as GDD) and is generally given in fs2. As a pulse travels through a material or coating and is reflected, the components are delayed depending on their frequency. If the GDD of a coating is 0 then the group delay is constant and the overall structure of the pulse is maintained. In a dispersive medium however, the pulse components travel at different speeds due to differing refractive indices for each wavelength (dispersion) implying a non-zero group delay dispersion. The result of this is that the pulse is broadened and also “chirped”.
To get around this, coatings can be designed such that they possess a low GDD or alternatively in some cases a pulse can be chirped artificially prior to reaching a mirror of opposite GDD such that the dispersion of the mirror corrects the chirped pulse structure. Quarter wave stacks typically have a low GDD across their high reflection bands making them useful for minimising broadening and chirping but less useful for correcting existing chirped-pulse structure.
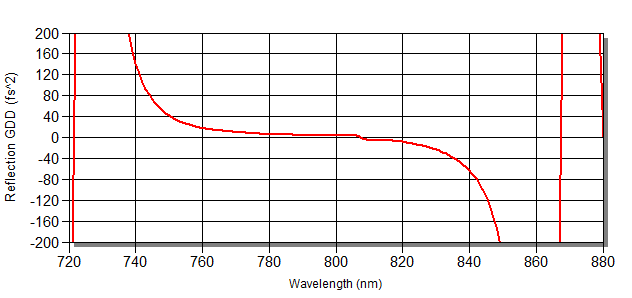
Figure 2: GDD of a 760-840nm mirror specially designed to have a low GDD across its high reflection band.
References and further reading
Thin Film Optical Filters Third Edition, H. A. Macleod, Institute of Physics publishing, J W Arrowsmith LtD. Bristol, 2001, ISBN 0 7503 06887 2
All Things Photonic VOL 2 Issue 1, CVI Melles Griot

